L’analyse statistique des résultats (ou des données) est indispensable pour faire des prévisions ou prendre des décisions autrement que par intuition.
Certaines méthodes permettent de définir la tendance d’évolution des résultats et de prévoir et de décider après une prévision plus ou moins intuitive des facteurs connus déterminants de l’évolution.
D’autres méthodes permettent de tester l’hypothèse que l’on fait concernant les facteurs de l’évolution des résultats
D’autres méthodes, enfin, permettent d’optimiser.
Explorons ces méthodes.
- La tendance base de la prévision.
Le graphique, indispensable, peut suggérer la tendance et on peut prévoir sommairement, sur cette base, selon ce que l’on pense de l’évolution des facteurs déterminants connus.
On peut aussi vouloir définir la tendance plus précisément et vérifier sa validité.
On sait que cette tendance peut être linéaire, exponentielle, logarithmique, puissance ou logistique et prendre l’une des allures présentées dans le tableau suivant
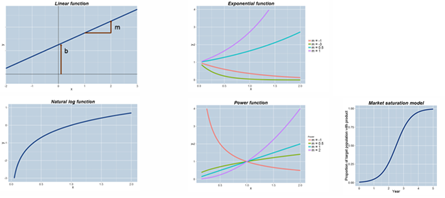
La tendance linéaire est la plus utilisée. On la trace en ajustant une droite qui soit la moins distante des résultats (droite des moindres carrées). C’est la méthode la plus facile mais aussi la plus trompeuse car on peut ajuster une droite dans n’importe quelle série de résultats et ne pas tenir compte des écarts entre les résultats et la tendance.
Le moyen de vérifier si c’est bien une tendance linéaire est de calculer le coefficient de corrélation entre les résultats et les valeurs correspondantes de la tendance et ce coefficient doit être proche de 1.
Il en va de même des autres tendances. On peut les tracer au jugé et se contenter de cela ou les déterminer avec précision et vérification en recourant à un tableur.
Prévoir sur la base de la tendance peut se faire après simple réflexion sur l’évolution probable des facteurs déterminants. Mais on peut aussi affiner cette prévision en estimant les résultats prévisionnels possibles et en leur affectant une probabilité de se réaliser ; cela ne fait pas disparaitre l’incertitude mais aide à décider.
On peut dire, par exemple, qu’on a 80% de chances que la tendance se prolonge et 10% qu’elle s’infléchisse vers le bas et 10% vers le haut (Loi normale).
Cela ne supprime pas l’incertitude mais permet de définir des scénarios.
- La régression base d’une prévision mieux fondée.
On sait que les résultats sont générés par des facteurs (décisions de l’entreprise ou autres) et on peut avoir l’intuition, plus ou moins fondée, d’en connaitre les principaux. La méthode de la régression, en fait de la corrélation, permet de tester ses hypothèses et de mieux fonder ses prévisions. Elle consiste à « croiser » la série des résultats avec la série d’un supposé facteur (régression simple) ou avec les séries de plusieurs facteurs (régression multiple). Il est alors facile de voir approximativement dans quelle mesure le facteur et les résultats sont « liés »
Le graphique ci-dessous ‘croise » le prix du diamant d’un poids donné avec la teneur en carat (pureté).
La liaison est évidente et linéaire et confirme ce que l’on sait ; le prix du diamant dépend de son carat.
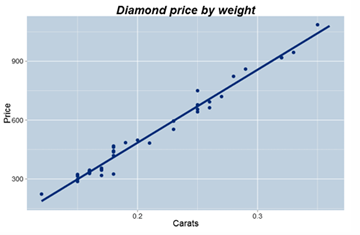
On peut alors tracer ou calculer par tableur la droite de régression (droite des moindres carrés) et faire une prévision de prix sans doute probable à 90%.
Evidemment, les choses ne sont pas aussi simples dans l’entreprise. Les liaisons sont moins « fortes » ce qui montre que d’autres facteurs ont aussi une influence. On peut tester la « liaison » des résultats avec plusieurs facteurs pris successivement ou simultanément (régression multiple) pour retenir celle qui est la plus forte comme base de prévision.
En fait la difficulté la plus grande de la prévision est ailleurs ; il ne sert à rien de trouver une liaison forte entre les résultats et un facteur si ce facteur est lui aussi difficile ou impossible à prévoir.
On ne peut prendre, alors, comme facteur que les décisions de l’entreprise ou celles de la concurrence ou les données sur la population.
Par ailleurs, il faut noter qu’il reste une dispersion des résultats autour de la droite ajustée (résidus) ; c’est-à-dire que la droite ne donne qu’une prédiction moyenne et qu’il faut estimer les probabilités que le résultat soit plus élevé ou plus bas.
On peut mesurer l’écart type des valeurs résiduelles (Root Mean Squared Error) pour comparer les « forces » des liaisons.
4.5 Transformer un ajustement d’une courbe en ligne.
Le graphique des résultats, ou de la liaison entre les résultats et un facteur, peut ne pas être linéaire mais curviligne. Lorsque qu’une courbe tend à passer plus près des points qu’une droite, il faut transformer les valeurs en logarithmes, tracer le graphique en log et vérifier qu’on retrouve un bon ajustement linéaire.
On peut alors utiliser les méthodes appliquées pour la corrélation linéaire.
L’inconvénient de cette méthode concerne la présentation devant un auditoire qui peut ne pas comprendre les logs.
Ce modèle de régression permet de prévoir le log de la valeur prévue avec la distribution de probabilité habituelle.
4.6 Régression multiple
Elle conduit à prendre en compte simultanément plusieurs facteurs déterminants ; par exemple vérifier si la consommation de carburant d’une voiture est expliquée, plus ou moins, par le poids de la voiture, la taille et la puissance du moteur.
On obtient alors un graphique en trois dimensions du type ci-dessous où chaque point représente une voiture.
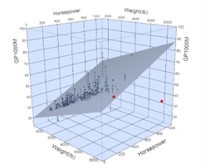
On a donc, maintenant, la valeur attendue de la consommation de carburant, compte tenu du poids et de la puissance du véhicule et l’équation de l’ajustement peut être calculée.
Et le meilleur ajustement est celui qui minimise le plus la somme des carrés de la distance verticale entre le point et le plan.
4.7 Régression logistique
Lorsque la variable de résultat est continue, la régression linéaire est appropriée. Mais certaines variables de résultats peuvent être discrètes ; par exemple une réponse OUI ou NON à une question telle que « le consommateur a-t-il acheté le produit ». Ces variables discrètes, dichotomique, sont fréquentes en marketing.
La régression logistique est utilisée pour estimer la probabilité de « réussite » d’une variable aléatoire, par exemple la probabilité qu’un consommateur achète le produit, sur la base de facteurs connus ou choisis.
C’est bien une régression mais le résultat est une probabilité de réussite.
Ainsi on peut, par exemple, vouloir vérifier si le nombre de plug-ins installés dans un site web est de nature à le rendre vulnérable au piratage ou autres effets négatifs.
On explore un nombre important de sites et on calcule quel pourcentage d’entre eux sont piratés ; on « croise » la proportion de sites piratés avec le nombre de plug-ins et on ajuste au mieux une courbe comme le montre le graphique ci-dessous : On voit que c’est une courbe logistique qui d’adapte le mieux.
C’est la courbe en S qui traduit une croissance exponentielle au début puis une tendance au plafonnement (cas de la diffusion d’un produit nouveau).
2.5 Optimisation
C’est l’une des préoccupations les plus importantes dans les entreprises.
Imaginons qu’on cherche à choisir le prix de vente qui maximise le profit.
On sait qu’en principe les ventes baissent ou augmentent si prix s’accroit ou baisse ? C’est l’élasticité des ventes aux prix.
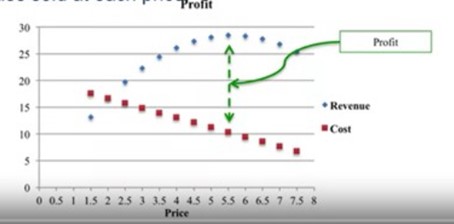
Quel est le meilleur prix à fixer pour maximiser mes profits ?
Si une augmentation de 1 % du prix est associée à une baisse de 2,5 % de la quantité demandée et si cette relation est proportionnelle, on peut trouver l’optimum comme le montre le graphique ci-dessus ou la courbe bleue représente l’évolution de la demande et la courbe rouge l’évolution des prix.
Le prix optimum est celui donne l’écart le grand avec la demande.
Source : https://www.coursera.org/learn/wharton-quantitative-modeling/home/module/1
Autres articles sur le sujet dans le blog :
https://outilspourdiriger.fr/trois-types-danalyse-des-donnees-necessaires-aux-managers/
https://outilspourdiriger.fr/methodes-de-lanalyse-des-donnees/
https://outilspourdiriger.fr/trois-types-analayse-donnees/
- Aucune reproduction ne peut être faite de cet article sans l’autorisation expresse de l’auteur. A. Uzan. 31/08/2025
